4 Degrees of Freedom Robot Arm With a Twist

4 Degrees of Freedom Robot Arm With a Twist

STM32F4 - Processor in the Loop
  • Inverse Kinematics of a Two-Link Planar Elbow Manipulator (Symbolic Math)
  • Solving the 4 Degree of Freedom (Matlab Script)
  • Simulink Matlab Function Block Implementation
  • Simulation with Simscape Multibody
  • Processor in the loop with STM32F4 Discovery Board
    • What we need
    • Results
  • Next Steps
This is a documentation of steps being done to be able to solve the 6 Degree of Freedom Robot Arm bought online. This goes through the process of solving the inverse kinematics of a Two-Link Planar Elbow Manipulator which is the basis of our case.

 Wrist and Clamps was not solve here &_&

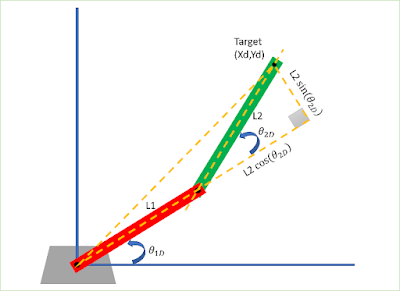
Inverse Kinematics of a Two-Link Planar Elbow Manipulator


 xd, yd = location of the tip of the manipulator    
q1d, q2d = angles of the links (counter-clockwise is positive) 
q3d = dummy angle
q4d = dummy angle
L1, L2 = lengths of the links (constant)
th1d := Symbol::subScript(Symbol("theta"),"1d"):
th2d := Symbol::subScript(Symbol("theta"),"2d"):
th3d := Symbol::subScript(Symbol("theta"),"3d"):
th4d := Symbol::subScript(Symbol("theta"),"4d"):
L1 := Symbol::subScript(Symbol("rho"),1):
L2 := Symbol::subScript(Symbol("rho"),2):
th1d, th2d, th3d, th4d, L1, L2;

Using Pythagoras theorem on the right triangle (law of cosines)
We can be able to add the L1 and L2cos(q2d) as X and L2sin(q2d) as Y
Since we have an assumption target location Xd and Yd we can be able to
solve q2d via Pythaoras theorem on the right triangle
eq1 := xd^2 + yd^2;
eq2 := L1 + (L2*(cos(th2d)));
eq3 := L2*sin(th2d);
eq4 := eq1 = eq2^2 + eq3^2
eq5 := simplify(eq4)
solving for cos(q2d)

assume(L1 > 0 and L2 > 0 ):
eq6 := op(solve(eq5,cos(th2d)),1);
q1D = q4D - q3D
eq7 := arccos(xd/(sqrt(xd^2 + yd^2)))
eq8 := L2*eq6
eq9 := cos(th3d) = (L1 + eq8)/sqrt(eq1)
eq10 := op(solve(eq9,cos(th3d)),1);
eq11 := arccos(eq10)
eq12 := eq7 - eq11
eq13 := th2d = arccos(eq6)

TH1des := subs(eq12),L1 = L_1,L2 = L_2;
TH2des := subs(eq13),L1 = L_1,L2 = L_2;



Solving from the top:

newth1des = th1des+th2des;
newth2des = th1des;

Solving the 4 Degree of freedom:

This is to check that the solution that we have from the Symbolic Math Toolbox is correct or not
%% Solving for a 4 Degree of Freedom Robot ARM
% this is just an example of solving 4 DoF Robot ARM via making one link
% (Stationary) from 0 to 360

%% Define the Target Location
xt = 0.5;
yt = 0.5;
zt = 0.5;
%% Define your robot arm body parameters
l1 = 1;
l2 = 1;
l3 = 1;
h0 = 0;

%% Top view angle : th0 (base angle)
% solve for th0
th0 = atand(yt/xt);
if th0 < 0
    th0 = th0+180;
elseif isnan(th0)
    th0 = 90;
end
display(th0)
%% For loop for Visualization
% we need to imagine that we have moved into a different Dimention hence
% you can si that we have change the angle to line lenghts to ut and wt
wt = sqrt(xt^2 + yt^2);
% Find the distance from the base of the bicep to the target
dist2target = sqrt(wt^2 + (zt-h0)^2);
ut = sqrt(dist2target^2 - wt^2);

%solve for the angle
angle = atand(ut/wt);
for counter = 0:360
th1 = counter;
xb = l1*cosd(th1);
yb = l1*sind(th1);
% solve the th1des and th2des with the ik_doublelink that we have solved
% earlier from our MuPad
[th1des, th2des] = ik_doublelink_mathworks(wt-xb,ut-yb,l2,l3);

% This is just for Visualization, you only need to get the th1des and
% th2des (Solving X and Y)
xl2 = l2*cosd(th1des);
yl2 = l2*sind(th1des);
xl3 = l3*cosd(th1des+th2des);
yl3 = l3*sind(th1des+th2des);
%display the x,y and r value
display([wt ut dist2target])
display([th1 th1des th2des])

% translate to solve from the top
% basically we made a PARALLELOGRAM from the solution with th1des and th2des
% and the angle origin 0 is on the +X axis
newth1des = th1des+th2des;
newth2des = th1des;

newxl2 = l2*cosd(newth1des);
newyl2 = l2*sind(newth1des);

newxl3 = l3*cosd(newth2des);
newyl3 = l3*sind(newth2des);

subplot(1,2,1)
plot(wt,ut,'rx')
xlim([-1 2]);
ylim([-1 2]);
hold on
plot([0,xb],[0,yb])
plot([xb,xb+xl2],[yb,yb+yl2])
plot([xb+xl2,xb+xl2+xl3],[yb+yl2,yb+yl2+yl3])

subplot(1,2,2)
plot(wt,ut,'rx')
xlim([-1 2]);
ylim([-1 2]);
hold on
plot([0,xb],[0,yb])
plot([xb,xb+newxl2],[yb,yb+newyl2])
plot([xb+newxl2,xb+newxl2+newxl3],[yb+newyl2,yb+newyl2+newyl3])
pause(0.1)
end

This is for a fixed 45 Degree angle at the bicep

This is for a fixed 0-360 Degree angle at the bicep

Simulink Matlab Function Block Implementation:

function [tAngle,bAngle,fAngle,wAngle] = IK(xt,yt,zt)
%#codegen
persistent th0 th1 th2 th3
% Initialize joint angles on the first pass
if isempty(th0)
    th0 = 0;
    th1 = 60;
    th2 = 0;
    th3 = 0;
end

l1 = 1;
l2 = 1;
l3 = 1;
h0 = 0;

% solve for th0
th0 = 90 - atand(xt/yt);

if isnan(th0)
    th0 = 90;  
end

wt = sqrt(xt^2 + yt^2);
% Find the distance from the base of the bicep to the target
dist2target = sqrt(wt^2 + (zt-h0)^2);
ut = sqrt(dist2target^2 - wt^2);

%solve for the angle
%angle = atand(ut/wt);

xb = l1*cosd(th1);
yb = l1*sind(th1);

[th1des, th2des] = ik_doublelink_mathworks(wt-xb,ut-yb,l2,l3);

% translate to solve from the top
% basically we made a PARALLELOGRAM from the solution with th1des and th2des
% and the angle origin 0 is on the +X axis
th2 = th1des+th2des;
th3 = th1des;


tAngle = th0;
bAngle = th1;
fAngle = th2;
wAngle = th3;

end

function [th1des,th2des] = ik_doublelink_mathworks(xd,yd,l1,l2)
if sqrt(xd^2 + yd^2) < l1+l2
    % Calculate the forearm link angle
    c2 = (xd.^2 + yd.^2 - l1^2 - l2^2)/(2*l1*l2);
    s2 = sqrt(1 - c2.^2);
    th2des = atan2(s2, c2);
else % protect for relative floating point accuracy at th2 = 0
    c2 = 1;
    s2 = 0;
    th2des = 0;
end   

% Calculate the bicep link angle
k1 = l1 + l2*c2;
k2 = l2*s2;
% Mantain the sign of th1 positive
if xd < 0 && yd < 0 % if point is in the third quadrant add 2*pi
    th1des = 2*pi + atan2(yd, xd) - atan2(k2, k1);
else
    th1des = atan2(yd, xd) - atan2(k2, k1);
end

th1des = rad2deg(th1des);
th2des = rad2deg(th2des);
end

Simulation with Simscape Multi Body


Processor in the loop with STM32F4 Board

What we need:
  1. STM32F4Discovery Board
  2. USART Serial Converter (FTDI Basic)
  3. Two jumper wires for TX and RX
  4. STM32-Mat Support Package for Matlab/Simulink
  5. Matlab/Simulink License
    • Matlab
    • Simulink
    • Matlab Coder
    • Simulink Coder
    • Embedded Coder

Results: 
There is no difference between the simulation model and the code being generated and deployed to the STM32f4Discovery Board (Check Scope 2 Output)

The function IK is being called every 0.001 secs (fundamental timestep), according to the Code Execution profile of the IK function, the Maximum Execution time is around 339905 which we need to multiply by 1e-09 (Default time setting for the measurement) hence the IK Algorithm to solve the 4 DoF angles would take about 339.91 micro seconds hence calling the function every 1 milli seconds is enough to finish the function in solving the IK of the 4 DoF link arm.

Next Steps:

  • Conversion of the Degrees to Servo Motor Control Signal
  • Need to add in a 3.3v to 5.0v converter since the STM32Discovery Boards are operating at 3.3 volts
Credits to Mathworks and my Techsource AEG

How a Differential Equation Becomes a Robot

Comments

Post a Comment

Popular posts from this blog

[STM32F3] Hello World with STM32F3 Discovery - Part 2

Image
Setting up the hardware: I wanted to merge the examples provided by STM32-MAT/TARGET (STM32 embedded Target for Matlab/Simulink) and the common use case of System Identification Toolbox, Control System Toolbox and Simulink Control Design Toolbox of Mathworks. This will stream line the capabilities of the support package that the  STM32-MAT has provided and the available toolboxes with matlab to be able to develop a Switch Model Power Supply (Boost Converter). References would be on this links: STM32-MAT Target Support Package STM32F3348Discovery Website STM32F3348 Application Note HRTIM Cookbook Fig. 1 The STM32F3348 Discovery board has a buck boost converter on the pcb (Highlighted in red) Objective 1: Enable the boost section of the circuit with STM32CubeMX Based on the documentation of the STM32F3 Application note AN4449  we need to set TA1 (PA8) to high and TA2(PA9) to low. We also need to set the TB1(PA10) to PWM output and TB2(PA11) to the com...
Read more

[STM32F3] Hello World with STM32F3 Discovery - Part 3

Image
Checks on the Peripherals As being discussed in the previous post, we can already use the blocks that is provided by the STM32-MAT support package from STMicroelectronics. Further more we will be checking if we have set the configuration correctly and the register values accordingly.  Learning the effects of a certain configuration will let us understand each parameters of the STM32CubeMX for the STM32F3348Discovery. Hardware and Software needed: Fig. 1 Needed Hardware/Software Matlab/Simulink with Embedded Coder Oscilloscope (2 Channels would be sufficient) STM32F3348 Discovery Board GPIB Cable (depends on your oscilloscope) 5 Volts Power Supply HRTIM TimerB The key point why we will use the HRTIM timer is that we can be able to achieve higher PWM Frequency. Normally SMPS has around 100kHz to 4MHz of operating frequency. For our case we will be setting the  HRTIM Timber B PWM Period to 250kHz and a Repetition IRQ on every 16 or 32 cycles of our P...
Read more

[STM32F3] Hello World with STM32F3 Discovery - Part 4

Image
Open loop Boost Converter to Close loop Boost Converter As what we have discussed and talked about in part 3 of this blog series, we are now going to have an open loop controller first before we can properly set our PI Close loop Control System. With our duty cycle percentage value and the voltage output due to that duty cycle percentage we can then use System Identification Toolbox of Matlab to get the transfer function of the design under test. However we still need Instrument Control Toolbox to be able to bring the snapshot of our oscilloscope to Matlab. Open Loop Boost Converter Fig. 1 Connections for the Open Loop To simply our open loop response a step block will be used that will issue a value of  9216 which is equivalent to 50% duty cycle Fig. 2 Open Loop Model Channel 1 which is connected to the Boost Converter Output has a value of 10 Volts and Channel 2 which is connected to the DAC PA4 output has a value of 1.64 (~ 50% of 3.3 volts) Fig. 3 Step Re...
Read more